Answer:
681 feet
Explanation:
Let x represent the distance between campsite and the base of the cliff.
We have been given that Haylee hikes to the top of a 120-foot vertical cliff. From the top of the cliff, the angle of depression to her campsite is 10∘. We are asked to find the distance between campsite and the base of the cliff.
We can see that angle of depression forms a right triangle with respect to ground, cliff and campsite.
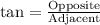
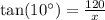
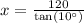
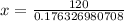
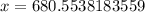
Upon rounding to nearest foot, we will get:
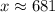
Therefore, the campsite is 681 feet away from the base of the cliff.