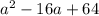Answer:
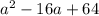
Explanation:
we have the options
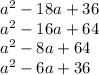
the one that is a perfect equare tinomial is:
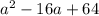
because we can rewrite this as follows:
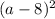 this is because we know that
this is because we know that
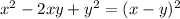
thus
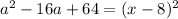
and the other options cannot be represented as a perfect square trinomial, so the correct answer is: