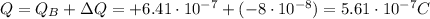a)
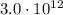
b)
Step-by-step explanation:
a)
The charge on one electron is negative and equal to the fundamental charge, so the charge on one electron is

Protons instead are positively charged particles, so they have a charge of
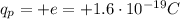
This means that the net charge of an object can be written as follows:
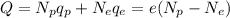
where:
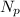 is the number of protons
is the number of protons
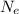 is the number of electrons
is the number of electrons
This can also be rewritten as
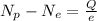
This equation gives the difference between the number of protons and the number of electrons in an object.
In this problem, object A has a charge of:

Substituting, we find
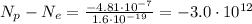
So, before the two objects come in contact, object A has
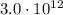 electrons more than protons.
electrons more than protons.
b)
When the two objects are touched together, the number of electrons transferred from object A to object B is:
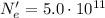
So the total charge transferred from object A to object is
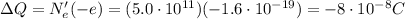
At the beginning, object B has a charge of:
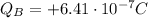
So, the final charge on object B after the electrons are transferred will be: