Answer:
3060 ways.
Explanation:
Given:
A certain company has 18 equally qualified applicants for 4 open positions.
Question asked:
How many different groups of 4 applicants can be chosen by the company to fill the positions if the order of selection does not matter?
Solution:
As mentioned that the order is not important, we will apply formula of combination.
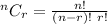
Number of different groups of 4 applicants can be chosen out of 18 in =
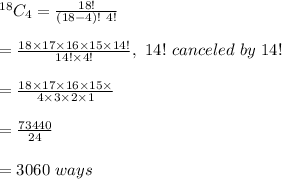
Therefore, different groups of 4 applicants can be chosen by the company in 3060 ways.