Answer:
The final temperature is 225.205 °C
Step-by-step explanation:
We have given
 = 60 °C = 333.15 K Initial temperature
= 60 °C = 333.15 K Initial temperature
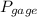 = 300 kPa , gage initial pressure ,
= 300 kPa , gage initial pressure ,
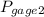 = 600 kPa , gage final pressure ,
= 600 kPa , gage final pressure ,
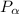 = 101.325 kPa
= 101.325 kPa
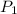 =
=
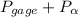
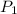 =
=
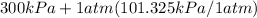
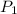 = 401.299 kPa.
= 401.299 kPa.
And
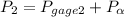
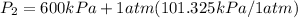
 600. 299 kPa
600. 299 kPa
So according to ideal gas Model
 this is equation one
this is equation one
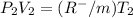 this is equation two
this is equation two
so By dividing equation two with equation one we get

putting values we get
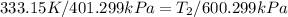
 = 225.205 °C
= 225.205 °C
This is final temperature