Question

Air flows steadily through a smooth, converging nozzle. At a location where the cross-sectional flow area is equal to 1.0 ft2, the pressure is equal to 115 psia, the temperature is 212 deg F, and the velocity is 250 ft/s. At a second location, downstream from the first, the area is equal to 85 in2. Compute the Mach number and velocity at this section.

Answer 1

The Mach number M₂ is 0.351636 and the velocity, V₂ is 445.15 ft/s

Step-by-step explanation:

Here we have

Temperature = 212 °F = 373.15 K

Pressure = 115 psia

Velocity = 250 ft/s = 72.6 m/s

Area, A₁ = 1 ft² = 0.09290304 m²

Mach number, M = V/c

c = √(γRT)

γ for air at 212 °F and 115 psia is 1.03/0.7412 =1.39

R for air = 287.05 J/kg K

Therefore, c = √(1.39·287.05·373.15) = 385.86 m/s

Mach number = V/c = 72.6/385.86 = 0.197

Therefore,

`(A_1)/(A^*) = (1)/(M_1) [(2)/((\gamma +1)) (1+((\gamma -1))/(2) M_1^2)]^{((\gamma +1))/(2(\gamma -1)) }`

Where

Which gives the area at the throat as

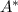`A^*` = 3.09×10⁻² m²

For the section with Area = 85 in² = 0.0548386 m²

We have

From

`(A_1)/(A^*) = (1)/(M_1) [(2)/((\gamma +1)) (1+((\gamma -1))/(2) M_1^2)]^{((\gamma +1))/(2(\gamma -1)) }`

Where:

A₂ = 0.0548386 m²

γ = 1.39

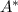`A^*` = 3.09×10⁻² m² Plugging in the values, we obtain M as

M₂ = 0.351636

Where the speed of sound is given by

c = V₂/M₂ = 385.86 m/s

V₂ = M₂ × 385.86 m/s = 0.351636 × 385.86 m/s = 135.682 m/s

V₂ = 135.682 m/s or 445.15 ft/s

The Mach number M₂ = 0.351636 and the velocity, V₂ = 445.15 ft/s.

Answer 2

match number at location 1 = 0.197

velocity at location1 =

velocity at location 2 = 356.56 fhz

match number at location 2 = 0.282

Step-by-step explanation:

check the attachment for the solution