Answer:
Dale will reach his goal at an annual rate of 11.83%.
Explanation:
The formula for continuos compounding is given by:

In which A is the amount after t years, P is the principal(initial amount) and r is the annual rate.
Dale has 2000 dollars to invest.
This means that
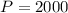
He has a goal to have 5800 in this invest ment in 9 years.
So
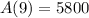
At what annual rate compounded continuously will Dale reach his goal?
This is r.

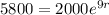
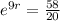
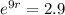
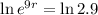
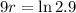

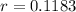
Dale will reach his goal at an annual rate of 11.83%.