Question

Ask Your Teacher A journal article reports that a sample of size 5 was used as a basis for calculating a 95% CI for the true average natural frequency (Hz) of delaminated beams of a certain type. The resulting interval was (229.266, 233.002). You decide that a confidence level of 99% is more appropriate than the 95% level used. What are the limits of the 99% interval? [Hint: Use the center of the interval and its width to determine x and s.] (Round your answers to three decimal places.)

Answer 1

The 99% confidence interval is (228.035, 234.233).

Explanation:

The sample size selected to compute the 95% confidence interval for the true average natural frequency (Hz) of delaminated beams of a certain type is

n = 5

The sample size is very small and the population standard deviation is also not known.

So, we will use t-interval for the confidence interval.

The (1 - α)% confidence interval for the true mean is:

`CI=\bar x\pm t_(\alpha/2, (n-1))* (s)/(√(n))`

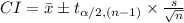
The 95% confidence interval for the true average natural frequency (Hz) of delaminated beams of a certain type is:

(Upper limit, Lower limit) = (229.266, 233.002).

Compute the value of sample mean as follows:

`\bar x=(UL+LL)/(2)=(233.002+229.266)/(2)=231.134`

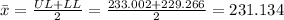
The critical value of t for α = 0.05 and n = 5 is:

`t_(\alpha/2, (n-1))=t_(0.05/2, (5-1))=t_(0.025,4)=2.776`

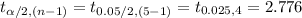
*Use a t-table.

Compute the value of sample standard deviation as follows:

`(UL-LL)/(2)=t_(\alpha/2, (n-1))* (s)/(√(n))\\(233.002-229.266)/(2)=2.776*(s)/(√(5))\\s=1.505`

The critical value of t for α = 0.01 and n = 5 is:

`t_(\alpha/2, (n-1))=t_(0.01/2, (5-1))=t_(0.005,4)=4.604`

*Use a t-table.

Construct the 99% confidence interval as follows:

`CI=\bar x\pm t_(\alpha/2, (n-1))* (s)/(√(n))\\=231.134\pm 4.604* (1.505)/(√(5))\\=231.134\pm3.099\\=(228.035, 234.233)`

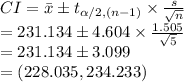
Thus, the 99% confidence interval is (228.035, 234.233).