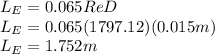Question

Air at 20 kPa and 5 °C enters a 1.5 cm diameter tube at a uniform velocity of 1.5 m/s. The tube walls are maintained at a uniform temperature of 45 °C. Estimate the distance from the entrance at which the flow becomes fully developed.

Answer 1

The distance from the entrance at which the flow becomes fully developed (entrance lenght) is:

`L_(E)=1.752 m`

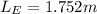
Step-by-step explanation:

First, we need to know if the flow is laminar or turbulent using the equation for the Reynolds number in a circular tube, which is:

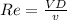`Re=(VD)/(v)` (Equation 1)

We know that for

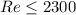`Re\leq 2300`, the flow is laminar

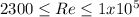`2300\leq Re\leq 1x10^(5)`, the flow is turbulent

Then, tanking into account that for air at 20 kPa and 5°C, kinematic viscosity
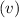`(v)` is
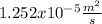`1.252x10^(-5) (m^(2))/(s)` (taken from Table A-9, Cengel's book), we use the equation 1 ,

`Re=((1.5 m/s)(0.015m))/(1.252x10^(-5)m^(2)/s)=1797.12`

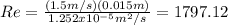
And, we can conclude that the flow is laminar. Then, we can use the relationship between the entrance length
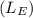`(L_(E))`, which is the distance from the entrance at wich the flow becomes fully developed, and diameter for a laminar flow in a circular tube, which is:

`(L_(E))/(D)=0.065Re`

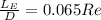
And we obtain,

`L_(E)=0.065ReD\\L_(E)=0.065(1797.12)(0.015 m)\\L_(E)=1.752m`