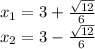Answer:
b. x=2,3,4
c.
x=2 is a local minimum
x=3 is a local maximum
x=4 is a local minimum
d.
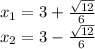
Explanation:
a. You have the function
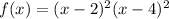
to find the intervals you have to take into account the roots of f(x), in this case you have the roots

- for x < 2, for example x=1:
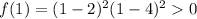
f(x) decreases from infinity to zero
- for 2 < x < 4, for example x=3:
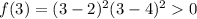
between x=2 and x=3 f(x) increases. But between x=3 and x=4 f(x) decreases because f(4)=0.
- for x > 4:
f(5)>0
f(x) increases for x > 4.
b. You have to compute the derivative to find local minima and maxima
![f'(x)=2(x-2)(x-4)^2+2(x-2)^2(x-4)=2(x-2)(x-4)[(x-4)+(x-2)]\\f'(x)=2(x-2)(x-4)(2x-6)](https://img.qammunity.org/2021/formulas/mathematics/college/zq2mbia8jvr4x1418wk1vciz7qnx9vfvzi.png)
and by taking f'(x)=0:
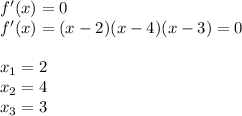
Local minima and maxima are found by evaluating the roots of f'(x) in the second derivative f''(x)
![f''(x)=2[(x-4)(2x-6)+(x-2)(2x-6)+(x-2)(x-4)(2)]\\f''(x)=2[2x^2-14x+24+2x^2-10x+12+2x^2-12x+16]\\f''(x)=12x^2-72x+104](https://img.qammunity.org/2021/formulas/mathematics/college/1f5oz9jc3t4ftrromybbdnn81avqkj71kp.png)
Hence
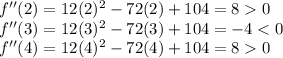
x=2 is a local minimum
x=3 is a local maximum
x=4 is a local minimum
c.
to find the concavity you have to find the inflection points
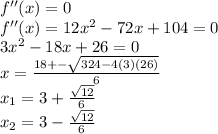
Hence:
for -infinity < x < x1 --> concave up
for x1 < x < x2 --> concave down
for x2 < x < infinity --> concave up
d.