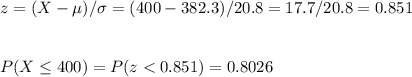Question

The shear strength of each of ten test spot welds is determined, yielding the following data (psi).

389 405 409 367 358 415 376 375 367 362

(a) Assuming that shear strength is normally distributed, estimate the true average shear strength and standard deviation of shear strength using the method of maximum likelihood. (Round your answers to two decimal places.)

average 382.3 psi
standard deviation 20.8 psi

(b) Again assuming a normal distribution, estimate the strength value below which 95% of all welds will have their strengths. [Hint: What is the 95th percentile in terms of μ and σ? Now use the invariance principle.] (Round your answer to two decimal places.)

________________________psi

(c) Suppose we decide to examine another test spot weld. Let X = shear strength of the weld. Use the given data to obtain the mle of P(X ≤ 400). [Hint:

P(X ≤ 400) = Φ((400 − μ)/σ).]

(Round your answer to four decimal places.)

___________.

Answer 1

a) Mean = 382.3 psi

Standard deviation = 20.8 psi

b) 392.7 psi

c) P(X<400)=0.8026

Explanation:

a) The population mean can be estimated as equal to the mean of the sample, and the population standard deviation can be estimated from the sample standard deviation:

`M=(1)/(n)\sum x_i=(1)/(10)(389+405+409+367+358+415+376+375+367+362)\\\\M=(1)/(10)(3823)=382.3\\\\\mu\approx M=382.3`

`s=\sqrt{(1)/(n-1)\sum (x_i-M)^2}=\sqrt{(1)/(10-1)(389-382.3)^2+...+(362-383.2)^2}\\\\\\s=\sqrt{(1)/(9)(3906.1)}=√(434)=20.8\\\\\\\sigma\approx s=20.8`

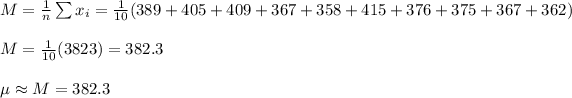
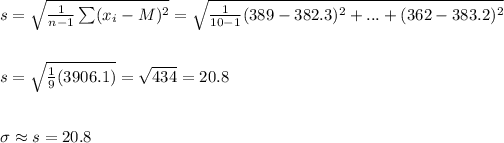
b) We start by searching for the z-value for the 95th percentile. This value is

z=1.645:

`P(z<1.645)=0.95`

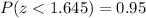
Then, the strength value below which 95% of all welds will have their strengths is:

`X=\mu+z\cdot \sigma/√(n)=382.3+1.645*20.8/√(10)\\\\X=382.3+32.9/3.2=382.3+10.4\\\\X=392.7`

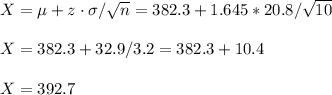
c) We calculate the probability of X being equal or less than 400 as:

`z=(X-\mu)/\sigma=(400-382.3)/20.8=17.7/20.8=0.851\\\\\\P(X\leq400)=P(z<0.851)=0.8026`