Answer:
a) Mean = 382.3 psi
Standard deviation = 20.8 psi
b) 392.7 psi
c) P(X<400)=0.8026
Explanation:
a) The population mean can be estimated as equal to the mean of the sample, and the population standard deviation can be estimated from the sample standard deviation:
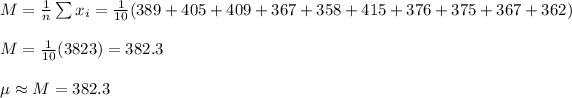
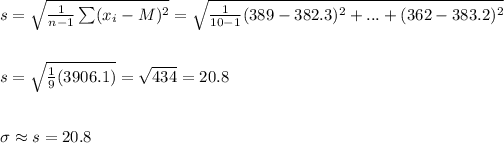
b) We start by searching for the z-value for the 95th percentile. This value is
z=1.645:
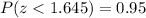
Then, the strength value below which 95% of all welds will have their strengths is:
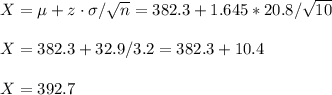
c) We calculate the probability of X being equal or less than 400 as:
