Question

The sides of a square field are 28 meters. A sprinkler in the center of the field sprays a circular area with a diameter that corresponds to a side of the field. How much of the field is not reached by the sprinkler

Answer 1

168.56

Explanation:

The answer is on the picture below. :)

Answer 2

The area of he field that is not reached by the sprinkler = 168.56
`m^(2)`

Explanation:

Side of the square field (a) = 28 m

Diameter of circular area (D) = 28 m

Radius of circular area (r)= 14 m

Area made by square field
`A_(1) = a^(2)`

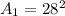`A_(1) = 28^(2)` = 784
`m^(2)`

Area made by circular field
`A_(2) = \pi r^(2)`

`A_(2) = \pi 14^(2)`

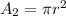
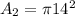
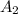`A_(2)` = 615.44
`m^(2)`

Field is not reached by the sprinkler A' =
`A_(1) - A_(2)`

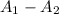
Put the values of
`A_(1)` &
`A_(2)`

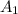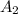
A' = 784 - 615.44

A' = 168.56
`m^(2)`

Therefore the area of he field that is not reached by the sprinkler = 168.56
`m^(2)`