Here is the full question
A coil consisting of 100 circular loops with radius 0.6 m carries a 5.0-A current.
(a) Find the magnetic field at a point along the axis of the coil, 0.80 m from the center.
(b) Along the axis, at what distance from the center of the coil is the field magnitude 1/8 as great as it is at the center
Answer:
a) B = 0.000113 T
b) The distance (x) from the center of the coil = 1.038 m
Step-by-step explanation:
The formula for the magnetic field on the line of axis of the circular loop can be expressed as:
B =

where;
N = number of turns = 100
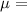
I = current flowing through the coil = 5.0- A
r = radius of the circular loop = 0.6 m
x = distance from the center of the coil
So;
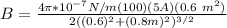
B = 0.000113 T
b)
Also; to determine the distance (x) from the center of the coil; we have the following:
We know that the magnetic field at the center of the coil can be expressed as:
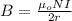
Now; given that the field magnitude is 1/8 as great as it is at the center; Then ;
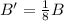
∴
 =
=
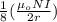
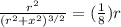
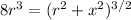
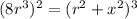
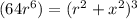
![(r^2+x^2) = \sqrt[3]{64r^6}](https://img.qammunity.org/2021/formulas/physics/college/d6kgwvaqtmuz1c58bzqdftc31jqxqvugr6.png)
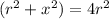
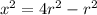
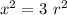
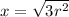
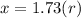
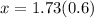
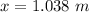
Therefore, the distance from the center of the coil is = 1.038 m