Answer:
a)
![\mathrm{E}[\mathrm{T}]=\sum_{\mathrm{H}}^(5) (200)/(101-i)](https://img.qammunity.org/2021/formulas/mathematics/high-school/f3fj98ws6pmruti4jh8af7a09s69c1rto6.png)
b)
![\mathrm{Var}[\mathrm{T}]=\sum_(k=1)^(5) ((200)^(2))/((101-i)^(2))](https://img.qammunity.org/2021/formulas/mathematics/high-school/yjvts4ftgqbxxanvtvn5es7s2fboubrqwf.png)
Explanation:
Given:
The lifetimes of the individual items are independent exponential random variables.
Mean = 200 hours.
Assume, Ti be the time between (
 )st and the
)st and the
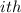 failures. Then, the
failures. Then, the
 are independent with
are independent with
 being exponential with rate
being exponential with rate

Therefore,
a)
![E[T]=\sum_(i=1)^(5) E\left[\tau_(i)\right]](https://img.qammunity.org/2021/formulas/mathematics/high-school/vun6l05vt75l2cswqmtovw0brd95ty98t0.png)
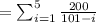
![\therefore \mathrm{E}[\mathrm{T}]=\sum_{\mathrm{H}}^(5) (200)/(101-i)](https://img.qammunity.org/2021/formulas/mathematics/high-school/l79qtdfg8qs9rufjihdwm7t4rqdg77vsjg.png)
The variance is given by,
![\mathrm{Var}[\mathrm{T}]=\sum_(i=1)^(5) \mathrm{Var}[T]](https://img.qammunity.org/2021/formulas/mathematics/high-school/8e4kh6nux4e072s8r4vxonh8px8rtk57id.png)
![\therefore \mathrm{Var}[\mathrm{T}]=\sum_(k=1)^(5) ((200)^(2))/((101-i)^(2))](https://img.qammunity.org/2021/formulas/mathematics/high-school/wfz8ia7bcv2qy0buw2prd8jero1csbcxr0.png)