Question

One hundred items are simultaneously put on a life test. Suppose the lifetimes

of the individual items are independent exponential random variables with mean 200 hours. The test will end when there have been a total of 5 failures. If T is the time at which the test ends,

(a) Find E[T].
(b) Find Var(T).

Answer 1

a)
`\mathrm{E}[\mathrm{T}]=\sum_{\mathrm{H}}^(5) (200)/(101-i)`

b)
`\mathrm{Var}[\mathrm{T}]=\sum_(k=1)^(5) ((200)^(2))/((101-i)^(2))`

Explanation:

Given:

The lifetimes of the individual items are independent exponential random variables.

Mean = 200 hours.

Assume, Ti be the time between (
`i-1` )st and the
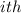`ith` failures. Then, the
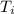`T_(i)` are independent with
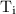`\mathrm{T}_{\mathrm{i}}` being exponential with rate
`((101-i))/(200) .`

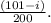
Therefore,

a)
`E[T]=\sum_(i=1)^(5) E\left[\tau_(i)\right]`

`=\sum_(i=1)^(5) (200)/(101-i)`

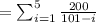
`\therefore \mathrm{E}[\mathrm{T}]=\sum_{\mathrm{H}}^(5) (200)/(101-i)`

`b)`

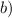
The variance is given by,
`\mathrm{Var}[\mathrm{T}]=\sum_(i=1)^(5) \mathrm{Var}[T]`

`\therefore \mathrm{Var}[\mathrm{T}]=\sum_(k=1)^(5) ((200)^(2))/((101-i)^(2))`