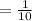Answer:
The required probability is
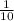 .
.
Explanation:
Probability:
The ratio of the favorable outcomes to the all possible outcomes.
Given that, in a bucket, there are 5 marbles red in color, 3 marbles blue in color and 2 marbles green in color.
Total number of marbles are = 5+3+2= 10
The probability that first marble was red

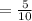
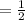
The probability that second marble was green is
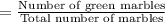
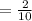
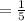
The required probability is