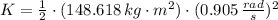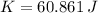Answer:
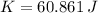
Step-by-step explanation:
The moment of inertia of the merry-go-round is:
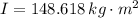
The tangential acceleration experimented by the merry-go-round is:
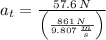
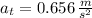
The linear speed after 2.54 seconds is determined hereafter:
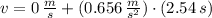
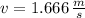
The angular speed of the merry-go-round is:
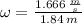
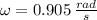
The kinetic energy due to the rotation for the merry-go-round is: