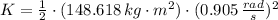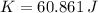Question

A horizontal 861 N merry-go-round of radius 1.84 m is started from rest by a constant horizontal force of 57.6 N applied tangentially to the merry-go-round. Find the kinetic energy of the merry-goround after 2.54 s. The acceleration of gravity is 9.8 m/s 2 . Assume the merry-go-round is a solid cylinder. Answer in units of J.

Answer 1

`K = 60.861\,J`

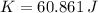
Step-by-step explanation:

The moment of inertia of the merry-go-round is:

`I = (1)/(2)\cdot \left((861\,N)/(9.807\,(m)/(s^(2)) ) \right)\cdot (1.84\,m)^(2)`

`I = 148.618\,kg\cdot m^(2)`

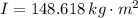
The tangential acceleration experimented by the merry-go-round is:

`a_(t) = (57.6\,N)/(\left((861\,N)/(9.807\,(m)/(s) )\right) )`

`a_(t) = 0.656\,(m)/(s^(2))`

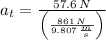
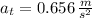
The linear speed after 2.54 seconds is determined hereafter:

`v = 0\,(m)/(s) + (0.656\,(m)/(s^(2)) )\cdot (2.54\,s)`

`v = 1.666\,(m)/(s)`

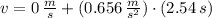
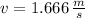
The angular speed of the merry-go-round is:

`\omega = (1.666\,(m)/(s) )/(1.84\,m)`

`\omega = 0.905\,(rad)/(s)`

The kinetic energy due to the rotation for the merry-go-round is:

`K =(1)/(2)\cdot (148.618\,kg\cdot m^(2))\cdot (0.905\,(rad)/(s) )^(2)`

`K = 60.861\,J`