Answer:
The probability of 4 successes,
P(X=4) =0.0660
Explanation:
Step 1:-
Let X be a binomial random variable with n = 9 and p = 0.2
probability of successes p = 0.2
probability of failure q = 1-p = 1-0.2 = 0.8
By using binomial distribution
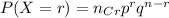
Step 2:-
The probability of 4 successes, i.e.,
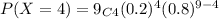
by using
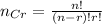
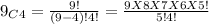
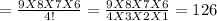
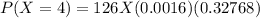
P(X=4) =0.0660
conclusion:-
The probability of 4 successes, that is P(X=4) =0.0660