Question

A toy helium balloon is initially at a temperature of T = 24o C. Its initial volume is 0.0042 m3 (It is a 10 cm radius sphere). Assume that the pressure in the balloon always equals atmospheric pressure, 101.3 kPa. 1)The balloon is lying in the sun, which causes the volume to expand by 13%. What is the new temperature, T? T =

Answer 1

The new temperature of the balloon is 27.12⁰C

Step-by-step explanation:

Given;

initial temperature of helium gas in balloon, T₁ = 24⁰ C

initial volume of the gas, V₁ = 0.0042 m³

pressure in the balloon, P = 101.3 kPa

The sun caused the balloon to expand by 13 % of the original volume; this implies that the original volume increased by 13%.

The new temperature, T₂ is calculated using general gas law;

`(P_1V_1)/(T_1) = (P_2V_2)/(T_2)`

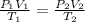
Since the pressure in the balloon is always equal, then P₁ = P₂

`(V_1)/(T_1) = (V_2)/(T_2)\\\\T_2 = (T_1V_2)/(V_1)\\\\T_2 =(24(0.0042\ +\ 0.13*0.0042))/(0.0042) \\\\T_2 = (24(0.004746))/(0.0042) \\\\T_2 = 27.12 \ ^oC`

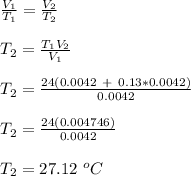
Therefore, the new temperature of the balloon is 27.12⁰C

Answer 2

`T_(f) = 335.780\,K\,(62.630\,^(\textdegree)C)`

Step-by-step explanation:

Let assume that air behaves ideally. The equation of state of ideal gases is:

`P\cdot V = n\cdot R_(u)\cdot T`

Where:

`P` - Pressure, in kPa.

`V` - Volume, in m³.

`n` - Quantity of moles, in kmol.

`R_(u)` - Ideal gas constant, in
`(kPa\cdot m^(3))/(kmol\cdot K)`.

`T` - Temperature, in K.

Since there is no changes in pressure or the quantity of moles, the following relationship between initial and final volumes and temperatures is built:

`(V_(o))/(T_(o)) = (V_(f))/(T_(f))`

The final temperature is:

`T_(f) = (V_(f))/(V_(o))\cdot T_(o)`

`T_(f) = 1.13\cdot (297.15\,K)`

`T_(f) = 335.780\,K\,(62.630\,^(\textdegree)C)`