Answer:
option (C) 16
Step-by-step explanation:
Data provided in the question:
Utility function is
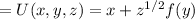
Number of tapes
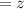
Number of tape recorders
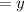
Amount of money
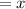
Left to spend
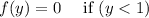
 is 1 or greater.
is 1 or greater.
The price of tapes is $1
The question states that she has one tape recorder. i.e.,
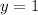
which means that
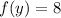 (since
(since
 then
then
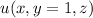
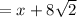
and

we take

condition for utility maximizing is.
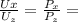
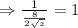
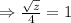
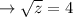
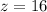
Hence, answer is option (C) 16