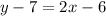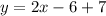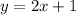Question

 which equation represents the line that passes through the points (3, 7) and (-1, -1)?

Answer 1

`y = 2x- 1`

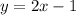
Explanation:

To determine which equation passes through the points (3, 7) and (-1, -1), we need to determine the slope of the equation. Then, we shall use point slope form to determine the equation of the line.

Determining the slope of the line:

`\text{Slope} = \frac{\text{Rise}}{\text{Run} } =\frac{\text{y}_(2) - \text{y}_(1) }{\text{x}_(2) - \text{x}_(1) }`

Substituting the points in the slope formula:

`\text{Slope} =(-1 - 7 )/(-1- 3 )`

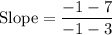
Simplifying the slope:

`\text{Slope} =(-1 - 7 )/(-1- 3 )`

`\text{Slope} =(-8)/(-4 ) = 2`

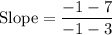
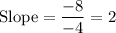
Determining the equation of the line:

We shall use point slope form to determine the equation of the line.

`\text{Point slope form:} \ y - y_(1) = m(x- x_(1) )`

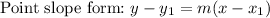
Substitute the slope and the coordinates of any two points stated above.

`y -7= 2(x- 3 ) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ [\text{Using the point (3,7)}]`

Simplify the equation and organize it to slope intercept form:

`y -7= 2x- 6`

`y = 2x- 6 + 7`

`y = 2x+ 1`

Answer 2

points: (3, 7) and (-1, -1)

slope (m) :

`\sf (y_2-y_1)/(x_2-x_1)`

========

`\hookrightarrow (-1-7)/(-1-3)`

`\hookrightarrow (-8)/(-4)`

`\hookrightarrow 2`

Equation:

`\sf y-y_1 = m(x-x_1)`

==============

`\rightarrow \sf y-7 = 2(x-3)`

`\rightarrow \sf y = 2x-6+7`

`\rightarrow \sf y = 2x+1`