The solution for the variable y is
 , if a given line passing through the point (12, -5) has a slope of
, if a given line passing through the point (12, -5) has a slope of
 .
.
Explanation:
The given is,
Point - (12, -5)
Slope -

Step:1
Formula for slope of line,
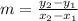 ...........................(1)
...........................(1)
Where,
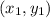 ,
,
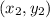 are points
are points
m - Slope
From given,
(12, -5) -
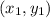
m =

Let, (x,y ) =
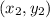
Equation (1) becomes,
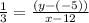
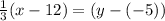
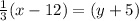

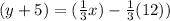
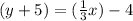
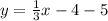
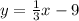
Result:
The solution for the variable y is
 , if a given line passing through the point (12, -5) has a slope of
, if a given line passing through the point (12, -5) has a slope of
 .
.