Question

a line passing through the point (12, - 5) has a slope of 1/3. Complete the work shown. Substitute known values for m, x1, and y1. Distribute the slope through the parentheses, solve for the y variable

Answer 1

the answer is -9

Explanation:

i took the test and got it right

Answer 2

The solution for the variable y is
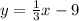`y=(1)/(3) x-9`, if a given line passing through the point (12, -5) has a slope of
`(1)/(3)`.

Explanation:

The given is,

Point - (12, -5)

Slope -
`(1)/(3)`

Step:1

Formula for slope of line,

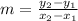`m = \frac{y_(2)-y_(1) } {x_(2) - x_(1) }`...........................(1)

Where,
`(x_(1) ,y_(1) )`,
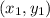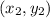`(x_(2) ,y_(2) )` are points

m - Slope

From given,

(12, -5) -
`(x_(1) ,y_(1) )`

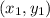
m =
`(1)/(3)`

Let, (x,y ) =
`(x_(2) ,y_(2) )`

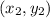
Equation (1) becomes,

`(1)/(3) = ((y - (-5)))/(x-12)`

`(1)/(3) (x-12) = (y-(-5))`

`(1)/(3) (x-12) = (y+5)`

`(y+5) = (1)/(3) (x-12)`

`(y+5) = ((1)/(3) x ) -(1)/(3)(12))`

`(y+5) = ((1)/(3) x ) -4`

`y = (1)/(3) x -4-5`

`y = (1)/(3) x -9`

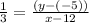
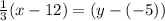
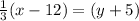
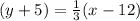
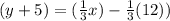
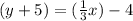
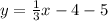
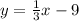
Result:

The solution for the variable y is
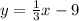`y=(1)/(3) x-9`, if a given line passing through the point (12, -5) has a slope of
`(1)/(3)`.