Answer:
a
The rate of work developed is
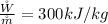
b
The rate of entropy produced within the turbine is

Step-by-step explanation:
From the question we are told
The rate at which heat is transferred is

the negative sign because the heat is transferred from the turbine
The specific heat capacity of air is

The inlet temperature is
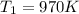
The outlet temperature is
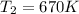
The pressure at the inlet of the turbine is
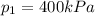
The pressure at the exist of the turbine is
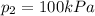
The temperature at outer surface is
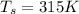
The individual gas constant of air R with a constant value
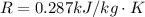
The general equation for the turbine operating at steady state is \
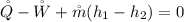
h is the enthalpy of the turbine and it is mathematically represented as
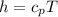
The above equation becomes
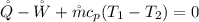

Where
 is the heat transfer from the turbine
is the heat transfer from the turbine
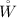 is the work output from the turbine
is the work output from the turbine
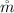 is the mass flow rate of air
is the mass flow rate of air
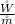 is the rate of work developed
is the rate of work developed
Substituting values
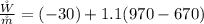
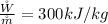
The general balance equation for an entropy rate is represented mathematically as

=>

generally
![(s_1 -s_2) = \Delta s = c_p\ ln[(T_2)/(T_1) ] + R \ ln[(v_2)/(v_1) ]](https://img.qammunity.org/2021/formulas/engineering/college/b29w49n8zmb6c52lagqvp8u2d8glpqzr8g.png)
substituting for
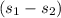
![(\sigma)/(\r m) = (-\r Q)/(\r m) * (1)/(T_s) + c_p\ ln[(T_2)/(T_1) ] - R \ ln[(p_2)/(p_1) ]](https://img.qammunity.org/2021/formulas/engineering/college/brtsaq1m25bu6suwj4qzvt6o9blquj3353.png)
Where
 is the rate of entropy produced within the turbine
is the rate of entropy produced within the turbine
substituting values
![(\sigma)/(\r m) = - (-30) * (1)/(315) + 1.1 * ln(670)/(970) - 0.287 * ln [(100kPa)/(400kPa) ]](https://img.qammunity.org/2021/formulas/engineering/college/8irg1fav3831w6iyr0le6p2wbes1e4pzqz.png)
