Question

When a survey asked subjects whether they would be willing to accept cuts in their standard of living to protect the​ environment, 328 of 1140 subjects said yes. a. Find the point estimate of the proportion of the population who would answer yes. b. Find the margin of error for a​ 95% confidence interval. c. Construct the​ 95% confidence interval for the population proportion. What do the numbers in this interval​ represent? d. State and check the assumptions needed for the interval in ​(c) to be valid.

Answer 1

`a.\ \hat p=0.2877\\\\b.\ ME=0.0263\\\\c.\ 0.2614<\hat p<0.3140`

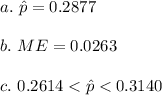
d. -Sample selection was random

-Individual observations are independent of each other

np≥10

Explanation:

a. The point estimate of a sample proportion is obtained using the formula;

`\hat p=(x)/(n)\\\\x-sample \ size\\n-population\ size\\\hat p-point \ estimate\\\\\\\\\therefore \hat p=(328)/(1140)\\\\\\=0.2877`

Hence, the point estimate of the proportion of the population is 0.2877

b. The desired margin of error is the calculated using the point estimate value as follows:

`ME=z\sqrt{(\hat p(1-\hat p))/(n)}\\\\z_(0.025)=1.96\\\\\hat p=0.2877\\\\\therefore ME=1.96* \sqrt{(0.2877(1-0.2877))/(1140)} \\\\=0.0263`

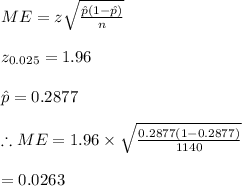
Hence, the desired margin of error for the sample proportion is 0.0263

c. Given a confidence level of 95%, the confidence interval can be calculated as:

`CI_(95\%)=\hat p\pm ME\\\\=0.2877\pm 0.0263\\\\=[0.2614,0.3140]`

Hence, the confidence interval at 95% confidence level is 0.2614<p<0.3140

#We are 95% confident that the interval estimate contains the desired proportion.

d. The assumptions are:

-The sample size is is more than 10 or equal to 10:

`n\hat p\geq 10\\n\hat p=0.2877* 328=94.37\geq 10\\\\\therefore np\geq 10`

-The selection was from a randomized experiment.

-The individual observations were independent of each other.