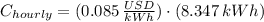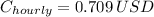Question

Fernando Mazzon asked Dec 14, 2021

37,456 views

2 Answers

Johnny Graber · Answer 1 · 2021-12-17T05:38:40+0000

Answer:

70.9 cents.

Step-by-step explanation:

Let assume that water at inlet is a saturated liquid. The process within pump is modelled after the First Law of Thermodynamics:

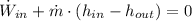
$\dot W_(in) + \dot m \cdot (h_(in)-h_(out)) = 0$

The power consumed by the pump is:

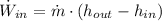
$\dot W_(in) = \dot m \cdot (h_(out)-h_(in))$

The isentropic effciency of the pump is:

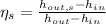
$\eta_(s) = (h_(out,s)-h_(in))/(h_(out)-h_(in))$

Where,

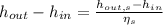
$h_(out) - h_(in) = (h_(out,s)-h_(in))/(\eta_(s))$

The power equation is modified into the following form:

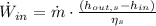
$\dot W_(in) = \dot m \cdot ((h_(out,s)-h_(in)))/(\eta_(s))$

Specific enthalpies and entropies at inlet and outlet are obtained from steam tables and included below:

State 1 (Saturated Liquid)

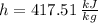
$h = 417.51\,(kJ)/(kg)$

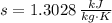
$s = 1.3028\,(kJ)/(kg\cdot K)$

State 2s (Subcooled Liquid)

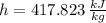
$h = 417.823\,(kJ)/(kg)$

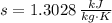
$s = 1.3028\,(kJ)/(kg\cdot K)$

The power consume by the pump is:

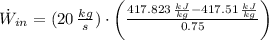
$\dot W_(in) = (20\,(kg)/(s) )\cdot \left((417.823\,(kJ)/(kg)-417.51\,(kJ)/(kg) )/(0.75) \right)$

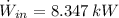
$\dot W_(in) = 8.347\,kW$

The hourly energy consumption is:

$E_(hourly) = (8.347\,kW)\cdot (3600\,s)\cdot \left((1\,kWh)/(3600\,kJ) \right)$

$E_(hourly) = 8.347\,kWh$

The hourly cost is:

$C_(hourly) = (0.085\,(USD)/(kWh) )\cdot (8.347\,kWh)$

$C_(hourly) = 0.709\,USD$

Please log in or register to add a comment.