Answer:
The minimum sample size must be 1118 to have margin of error within one percentage point.
Explanation:
We are given the following in the question:
Germination rate = 97% = 0.97
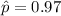
Margin of error = 1% = 0.01
We have to find the minimum sample size for a 95% confidence interval.
Formula for margin of error:


Putting values, we get,

Rounding off to integer,
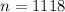
Thus, the minimum sample size must be 1118 to have margin of error within one percentage point.