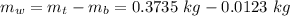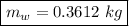Answer:
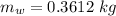
Step-by-step explanation:
Momentum and Energy
As the bullet-block system collide inelastically, the momentum is conserved before and after the collision. The energy is not conserved since the interaction is perfectly inelastic and part of the energy is lost in the change of shape when both masses stick together.
Once the system moves on a frictionless surface, the kinetic energy is transformed into elastic energy of the spring.
The elastic energy of a spring of constant k being stretched by a distance x is
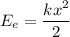
The block+bullet system compresses the spring by x=0.35 m, and the spring's constant is k=205 N/m, thus
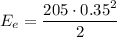
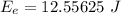
The kinetic energy of both masses is
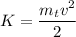
Where mt is the total mass of the block (unknown) and the bullet. Equating this energy to the elastic energy
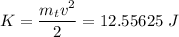
![\displaystyle (m_tv^2)/(2)=12.55625 \ J\text{..............[1]}](https://img.qammunity.org/2021/formulas/physics/college/g006mhov9024orxxlcs54d5bm5e7klmv4e.png)
Now consider the previous collision. The momentum before the collision is
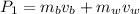
where mb is the mass of the bullet, mw the mass of the block, and vb, vw their respective speeds. Since the block is assumed to be at rest:
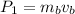
The mass of the bullet is mb=12.3 gr=0.0123 Kg and its speed vb=249 m/s, thus
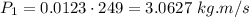
The final momentum is
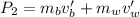
Since both objects remain together, vb'=vw'=v
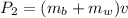
Equating both momentums
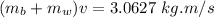
The total mass mt is the sum of both masses, thus
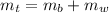
Therefore
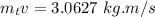
Solving for v
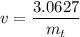
Replacing in [1]
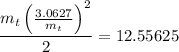
Operating and simplifying
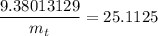
Solving for mt
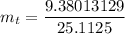
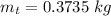
Finally, the mass of the block alone is