Question

Assume that military aircraft use ejection seats designed for men weighing between 146 lb and 212 lb. If​ women's weights are normally distributed with a mean of 173.3 lb and a standard deviation of 41.7 ​lb, what percentage of women have weights that are within those​ limits? Are many women excluded with those​ specifications?

Answer 1

56.69% of women belong within the given limits of seats. Yes, a majority of 43.31% of women are excluded with those​ specifications.

Explanation:

We are given the following information in the question:

Mean, μ = 173.3 lb

Standard Deviation, σ = 41.7 ​lb

We are given that the distribution of women's weight is a bell shaped distribution that is a normal distribution.

Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

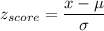
P(weighing between 146 lb and 212 lb)

`P(146 \leq x \leq 212)\\\\ = P(\displaystyle(146 - 173.3)/(41.7) \leq z \leq \displaystyle(212-173.3)/(41.7))\\\\ = P(-0.6546 \leq z \leq 0.9280)\\\\= P(z \leq 0.9280) - P(z < -0.6546)\\= 0.8233 -0.2564 = 0.5669 = 56.69\%`

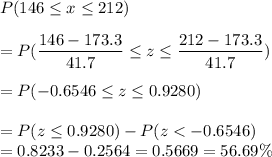
Thus, 56.69% of women belong within the given limits of seats. Yes, a majority of 43.31% of women are excluded with those​ specifications.