Question

Light from an argon laser strikes a diffraction grating that has 5,139 grooves per centimeter. The central and first-order principal maxima are separated by 0.488 m on a wall 1.78 m from the grating. Determine the wavelength of the laser light.

Answer 1

515.5 nm

Step-by-step explanation:

To find the wavelength (λ) of the laser light we can use the following equation:

`n\lambda = dsin(\theta)`

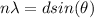
Where:

n: is the order of the principal maxima = 1

d: is the width of the groove = 1/N

N: is the number of grooves per length = 5139 grooves/cm

θ: is the angle made by the spectral line → tanθ = D/L

D: is the separation from the wall = 0.488 m

L: is the separation from the grating = 1.78 m

First, we have to find d and θ:

`d = (1)/(N) = (1)/(5139 grooves/cm)*(1 m)/(100 cm) = 1.95 \cdot 10^(-6) m`

`\theta = arctan((D)/(L)) = arctang ((0.488 m)/(1.78 m)) = 15.33 ^\circ`

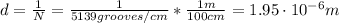
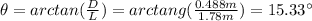
Now, we can calculate the wavelength of the laser light:

`\lambda = (dsin(\theta))/(n) = (1.95 \cdot 10^(-6) m*sin(15.33))/(1) = 5.155 \cdot 10^(-7) m = 515.5 nm`

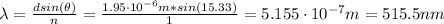
Therefore, the wavelength of the laser light is 515.5 nm.

I hope it helps you!