Answer:
515.5 nm
Step-by-step explanation:
To find the wavelength (λ) of the laser light we can use the following equation:
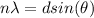
Where:
n: is the order of the principal maxima = 1
d: is the width of the groove = 1/N
N: is the number of grooves per length = 5139 grooves/cm
θ: is the angle made by the spectral line → tanθ = D/L
D: is the separation from the wall = 0.488 m
L: is the separation from the grating = 1.78 m
First, we have to find d and θ:
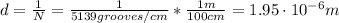
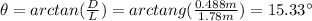
Now, we can calculate the wavelength of the laser light:
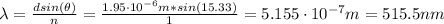
Therefore, the wavelength of the laser light is 515.5 nm.
I hope it helps you!