Question

An electric generator contains a coil of 130 turns of wire, each forming a rectangular loop 74.6 cm by 24.9 cm. The coil is placed entirely in a uniform magnetic field with magnitude B = 3.82 T and initially perpendicular to the coil's plane. What is in volts the maximum value of the emf produced when the loop is spun at 1120 rev/min about an axis perpendicular to the magnetic field?

Answer 1

The maximum value of the emf produced is 10819.098 V

Step-by-step explanation:

Given data:

N = number of turn = 130

The area is:

`A=74.6*24.9=1857.54cm^(2) =0.185754m^(2)`

B = magnetic field = 3.82 T

w = angular speed = 1120 rev/min = 117.286 rad/s

The maximum value of the emf produced is:

`E=BANw=3.82*0.185754*130*117.286=10819.098V`

Answer 2

10.85 kV

Explanation:

The maximum value of the emf (ε) produced can be calculated using Faraday's law equation:

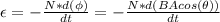`\epsilon = - (N*d(\phi))/(dt) = - (N*d(BAcos(\theta)))/(dt)` (1)

Where:

N: is the turns of wire = 130 turns

Φ: is the magnetic flux = BAcos(θ)

B: is the magnetic field = 3.82 T

A: is the area of the coil = a*b = 0.746 m*0.249 m = 0.186 m²

θ: is the angle between the magnetic field lines and the normal to A = ωt = 2πft

f: is the frequency = 1120 rev/min = 18.7 rev/s

From equation (1) we have:

`\epsilon_(max) = NBA2\pi f sin(2\pi ft) = NAB2\pi f = 130*0.186 m^(2)*3.82 T*2*\pi*18.7 rev/s = 10852.8 V = 10.85 kV`

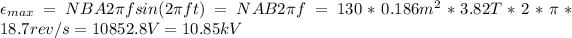
Therefore, the maximum value of the emf produced is 10.85 kV.

I hope it helps you!