Answer:
10.85 kV
Explanation:
The maximum value of the emf (ε) produced can be calculated using Faraday's law equation:
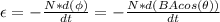 (1)
(1)
Where:
N: is the turns of wire = 130 turns
Φ: is the magnetic flux = BAcos(θ)
B: is the magnetic field = 3.82 T
A: is the area of the coil = a*b = 0.746 m*0.249 m = 0.186 m²
θ: is the angle between the magnetic field lines and the normal to A = ωt = 2πft
f: is the frequency = 1120 rev/min = 18.7 rev/s
From equation (1) we have:
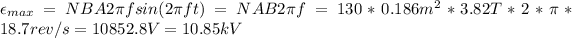
Therefore, the maximum value of the emf produced is 10.85 kV.
I hope it helps you!