Answer:
The population of the country will be 510 million during the year of 2018.
Explanation:
The exponential model for the population, in millions, t years after 2003 is.
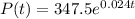
Use the model to determine when the population of the country will be 510 million.
t years after 2003, in which t is found when P(t) = 510. So
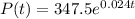
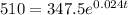
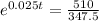
Applying ln to both sides, so we can find t
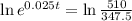
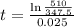
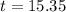
15.35 years after 2003, so during the year of 2018.
The population of the country will be 510 million during the year of 2018.