Answer:
If not caught, the football is in the air for about 3.83 seconds
Step-by-step explanation:
The quadratic function:
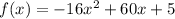
models the height of a football after x seconds, so we want to know how long the ball is in the air if not caught. The ball lands on the ground when
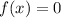 . Then, our equation becomes:
. Then, our equation becomes:
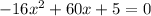
Using quadratic formula we can get the x-values that makes this equation to be true:
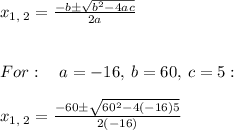

Since time can't be negative we discards
 so the only valid solution is
so the only valid solution is
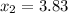 .
.
In conclusion: If not caught, the football is in the air for about 3.83 seconds