Question

a football coach uses a passing machine to simulate 50-yard passes during practice. the quadratic function f(x)=-16x+60x+5 models the height of the football after x seconds. how long is the football in the air if not caught?

Answer 1

If not caught, the football is in the air for about 3.83 seconds

Step-by-step explanation:

The quadratic function:

`f(x)=-16x^2+60x+5`

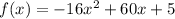
models the height of a football after x seconds, so we want to know how long the ball is in the air if not caught. The ball lands on the ground when
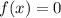`f(x)=0`. Then, our equation becomes:

`-16x^2+60x+5=0`

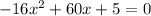
Using quadratic formula we can get the x-values that makes this equation to be true:

`x_(1,\:2)=(-b\pm √(b^2-4ac))/(2a) \\ \\ \\ For: \quad a=-16,\:b=60,\:c=5:\quad \\ \\ x_(1,\:2)=(-60\pm √(60^2-4\left(-16\right)5))/(2\left(-16\right))`

`Two \ solutions: \\ \\ x_(1)=(-60+√(60^2-4\left(-16\right)5))/(2\left(-16\right))=-(-15+7√(5))/(8)=-0.08 \\ \\ \\ x_(2)=(-60+√(60^2-4\left(-16\right)5))/(2\left(-16\right))= -(-15+7√(5))/(8)=3.83`

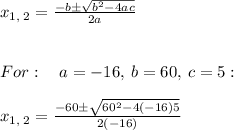
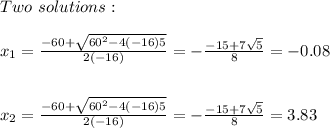
Since time can't be negative we discards
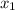`x_(1)` so the only valid solution is
`x_(2)=3.83`.

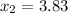In conclusion: If not caught, the football is in the air for about 3.83 seconds