Question

The wear resistance of a steel shaft is to be improved by hardening its surface by increasing the nitrogen (N) content within an outer surface layer as a result of nitrogen diffusion into the steel; the nitrogen is to be supplied from an external N-rich gas at an elevated and constant temperature. The initial N content of the steel is 0.0025 wt%, whereas the surface concentration is to be maintained at 0.45 wt%. For this treatment to be effective, a N content of 0.12 wt% must be established at a position 0.45 mm below the surface. (a) Will this process be a steady state or non-state process? Why?

Answer 1

Non steady state process

Because D ∝ 1/t

Step-by-step explanation:

Here we have

`(c_x -c_D)/(c_S-c_D) = 1-erf((x)/(2√(Dt) ) )`

Where:

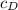`c_D` = 0.0025 % by weight of N

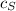`c_S` = 0.45 % by weight of N

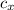`c_x` = 0.12 % by weight of N

Therefore,

`(0.12 -0.0025)/(0.45-0.0025) = 1-erf((x )/(2√(Dt) ) )= 0.2626`

`erf((x )/(2√(Dt) ) )= 1-0.2626 = 0.7374`

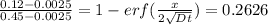
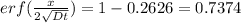
From the inverse erf function we have

`(x )/(2√(Dt) ) = 0.7921`

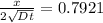
Since x = 0.45 mm, we have

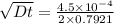`√(Dt) =(4.5*10^(-4))/(2* 0.7921)` and

Dt = 8.069×10⁻⁸ m²

`D_0exp(-Qd)/(RT) * t = 8.07*10^(-8) m^2`

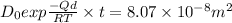
For steady state

`(dC)/(dt) =0 =D(d^2C)/(dx^2)`

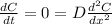
Since Dt = 8.069×10⁻⁸ m² = Constant, then as the time increases the diffusion rate decreases hence the process is not steady state.

D is inversely proportional to t.