Question

The random variable X is exponentially distributed, where X represents the time it takes for a person to choose a birthday gift. If X has an average value of 26 minutes, what is the probability that X is less than 30 minutes? (Do not round until the final step. Round your answer to 3 decimal places.)

Answer 1

0.685 = 68.5% probability that X is less than 30 minutes

Explanation:

Exponential distribution:

The exponential probability distribution, with mean m, is described by the following equation:

`f(x) = \mu e^(-\mu x)`

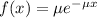
In which
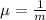`\mu = (1)/(m)` is the decay parameter.

The probability that x is lower or equal to a is given by:

`P(X \leq x) = \int\limits^a_0 {f(x)} \, dx`

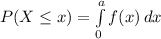
Which has the following solution:

`P(X \leq x) = 1 - e^(-\mu x)`

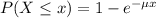
If X has an average value of 26 minutes

This means that
`m = 26, \mu = (1)/(26)`

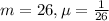
What is the probability that X is less than 30 minutes?

`P(X \leq 30) = 1 - e^{-(30)/(26)} = 0.685`

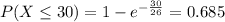
0.685 = 68.5% probability that X is less than 30 minutes