Question

As Halley’s comet orbits the sun, its distance from the sun changes dramatically. If the comet’s speed at a distance of 9.3 × 1010 m from the sun is 5.1 × 104 m/s and angular momentum is conserved, what is its speed when it is 4.0 × 1012 m from the sun?

Answer 1

Its speed is
`v_(b) = 1185m/s`.

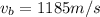Step-by-step explanation:

The angular momentum is defined as:

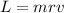`L = mrv` (1)

Since there is no torque acting on the system, it can be express in the following way:

`t = (\Delta L)/(\Delta t)`

`t \Delta t = \Delta L`

`\Delta L = 0`

`L_(a) - L_(b) = 0`

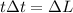
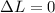
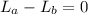
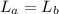`L_(a) = L_(b)` (2)

Replacing equation 1 in equation 2 it is gotten:

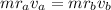`mr_(a)v_(a) =mr_(b)v_(b)` (3)

As can be seen in equation 3 the angular momentum is conserved.

Where m is the mass of the comet,
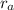`r_(a)` is the orbital radius when it is farther form the Sun,
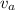`v_(a)` is the speed when is farther from the Sun,
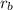`r_(b)` is the orbital radius when is closer to the Sun,
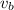`v_(b)` is the speed when it is closer to the Sun.

From equation 3
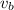`v_(b)` will be isolated:

`v_(b) = (mr_(a)v_(a))/(mr_(b))`

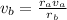`v_(b) = (r_(a)v_(a))/(r_(b))` (4)

`v_(b) = ((9.3x10^(10)m)(5.1x10^(4)m/s))/((4.0x10^(12)m))`

`v_(b) = 1185m/s`

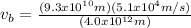
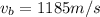
Hence, its speed is
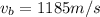`v_(b) = 1185m/s`.