Question

The diagram shows two vertical masts, AB and CD, on horizontal ground. The height of AB is 500m and the height of CD is 350m. The angle of elevation of B from D is 30 degrees. Calculate, to the nearest m, the distance AC.

Answer 1

To the nearest meter the distance AC is 260m

How to solve for the value of AC

The lines AB and CD, on horizontal ground.

The height of AB is 500 m.

The height of CD is 350 m.

The angle of elevation of B from D is 30°

We need to determine the distance AC.

To get AC we have to use the formula

AC = height of AB - height of CD / TAN θ

Here we would be finding the difference that first exists between the height of these two poles.

One pole is 500 m and the second pole is 350 meters

= 500 - 350 / tan θ

150 / tan 30

150 / 0.5773

= 259.8 m

Hence to the nearest meter the distance AC is 260m

Answer 2

Given:

The lines AB and CD, on horizontal ground.

The height of AB is 500 m.

The height of CD is 350 m.

The angle of elevation of B from D is 30°

We need to determine the distance AC.

Length of BE:

Let us construct a line that is parallel to AC.

Let the line be ED.

The length of BE is given by

`BE=AB-AE`

`BE=500-350`

`BE=150`

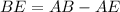
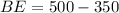
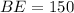
Thus, the length of BE is 150 m

Length of ED:

The length of ED can be determined using the trigonometric ratio.

Thus, we have;

`tan \ 30^(\circ)=(ED)/(BE)`

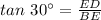
Substituting the values, we get;

`(√(3))/(3)=(ED)/(150)`

`(√(3))/(3)* 150=ED`

`50√(3)=ED`

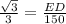
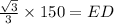
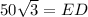
Thus, the length of ED is 50√3 m

Length of AC:

From the figure, it is obvious that the sides ED and AC have the equal length.

Thus, we have;

AC = ED = 50√3

Simplifying, we get;

`AC=50 * 1.732`

`AC=86.6 \ m`

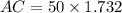
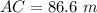
Hence, the length of AC is 86.6 m