Given:
The lines AB and CD, on horizontal ground.
The height of AB is 500 m.
The height of CD is 350 m.
The angle of elevation of B from D is 30°
We need to determine the distance AC.
Length of BE:
Let us construct a line that is parallel to AC.
Let the line be ED.
The length of BE is given by
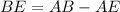
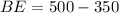
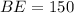
Thus, the length of BE is 150 m
Length of ED:
The length of ED can be determined using the trigonometric ratio.
Thus, we have;
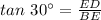
Substituting the values, we get;
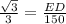
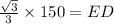
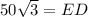
Thus, the length of ED is 50√3 m
Length of AC:
From the figure, it is obvious that the sides ED and AC have the equal length.
Thus, we have;
AC = ED = 50√3
Simplifying, we get;
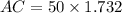
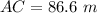
Hence, the length of AC is 86.6 m