Question

The floor of a railroad flatcar is loaded with loose crates having a coefficient of static friction of 0.25 with the floor. If the train is initially moving at a speed of 48 km/h, in how short a distance can the train be stopped at constant acceleration without causing the crates to slide over the floor

Answer 1

`x_(min)=36.2m`

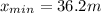
Step-by-step explanation:

The forces acting on the crates when the train starts stopping are their weights, the normal force from the train, the static frictional force and the fictional force that is produced by the deceleration of the train. As the gravitational force, this fictional force is equal to the mass of the crates multiplied by the magnitude of the acceleration of the train. So, the equations of motion of the crates will be:

`x: ma_t-f_s=0\implies f_s=ma_t\\\\y: N-mg=0\implies N=mg`

Since the static frictional force is
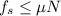`f_s\leq \mu N`, we get:

`ma_t\leq \mu mg\\\\\implies a_t\leq \mu g`

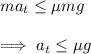
So we have a limit to the acceleration of the train. Now, we have to know the distance traveled by the train when it is stopping. Then, we use the kinematic formula:

`x=(v_0^(2))/(2a_t)`

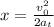
Now we solve for the acceleration to combine this equation to the inequality we got before:

`a_t=(v_0^(2))/(2x)\\ \\\implies (v_0^(2))/(2x)\leq \mu g`

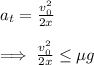
And solve for x:

`x\geq (v_0^(2))/(2\mu g)`

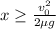
Since we are looking for the minimum value for x, we consider the case in which that inequality becomes an equation:

`x_(min)= (v_0^(2))/(2\mu g)`

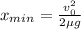
Before we finish, we have to convert the unities of the initial velocity to meters per second:

`48km/h=13.3m/s`

Finally, we plug in the known values to get
`x_(min)`:

`x_(min)=((13.3m/s)^(2))/(2(0.25)(9.8m/s^(2)))\\\\x_(min)=36.2m`

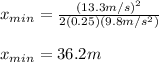
It means that the train can be stopped at a minimum distance of 36.2m at constant acceleration without causing the crates slide over the floor.