Question

Assume a warehouse operates 24 hours a day. Truck arrivals follow Poisson distribution with a mean rate of 36 per day and service (unloading using a single bay) operations follow exponential distribution with a rate of 48 trucks per day. What is the expected waiting time in the system (in hours) for a typical truck

Answer 1

The expected waiting time in system for typical truck is 2 hours.

Explanation:

Data Given are as follows.

Truck arrival rate is given by, α = 36 / day

Truck operation departure rate is given, β= 48 / day

A constructed queuing model is such that so that queue lengths and waiting time can be predicted.

In queuing theory, we have to achieve economic balance between number of customers arriving into system and that of leaving the system whether referring to people or things, in correlating such variables as how customers arrive, how service meets their requirements, average service time and extent of variations, and idle time.

This problem is solved by using concept of Single Channel Arrival with exponential service infinite populate model.

Waiting time in system is given by,

`w_(s) = (1)/(\alpha - \beta )`

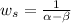
where
`w_s` is waiting time in system

`\alpha` is arrival rate described Poission distribution

`\beta` is service rate described by Exponential distribution

`w_(s) = (1)/(\alpha - \beta )`

`w_(s) = (1)/(48 - 36 )`

`w_(s) = (1)/(12 ) day`

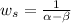
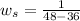
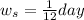
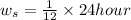`w_(s) = (1)/(12 ) * 24 hour` ...it is due to 1 day = 24 hours

`w_(s) = 2 hours`

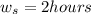
Therefore, time required for waiting in system is 2 hours.