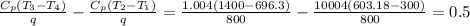Question

An ideal Brayton cycle has inlet air at 300 K, 100 kPa and the combustion process adds 800 kJ/kg. The maximum temperature is 1400 K due to material considerations. Using standard-air properties, find the maximum permissible compression ratio (pressure ratio across the compressor) and the cycle efficiency. The Cv and R of the air is 716 J/kg-K and 287 J/kg-K.

Answer 1

the maximum permissible compression ratio (pressure ratio across the compressor) r = 11.525 and the cycle efficiency (η) = 0.5

Step-by-step explanation:

`T_1 =300K\\ P_1=100kPa\\T_3=1400K\\q=800kJ/kq`

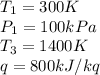
adiabatic exponent k = 1.4 and air specific heat
`C_p= 1.004kJ/kgK`

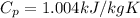
The specific heat transfer q is given by the equation:

`q=C_p(T_3-T_2)\\T_2=T_3-(q)/(C_p)`

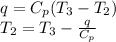
Substituting values:

`T_2=T_3-(q)/(C_p)= 1400-(800)/(1.004)= 603.18K`

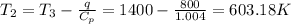
the maximum permissible compression ratio (pressure ratio across the compressor) r is given by:

`r = ((T_2)/(T_1) )^(k)/(k-1)`

Substituting values:

`r = ((T_2)/(T_1) )^(k)/(k-1) = ((603.18)/(300) )^(1.4)/(1.4-1)= 11.525`

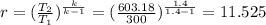
r = 11.525

Exhaust temperature (
`T_4`) =
`T_3(r^(1-k)/(k))`

`T_4=T_3(r^(1-k)/(k))=1400(11.525^(1-1.4)/(1.4)) =696.3K`

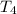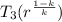
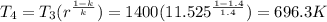
the cycle efficiency (η) =
`(C_p(T_3-T_4))/(q) - (C_p(T_2-T_1))/(q)`

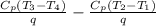
η =
`(C_p(T_3-T_4))/(q) - (C_p(T_2-T_1))/(q)= (1.004(1400-696.3))/(800) - (10004(603.18-300))/(800)=0.5`