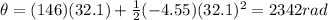Question

A disk, initially rotating at 146 rad/s, is slowed down with a constant angular acceleration of magnitude 4.55 rad/s2. (a) How much time does the disk take to stop? (b) Through what angle (rad) does the disk rotate during that time?

Answer 1

a) 32.1 s

b) 2342 rad

Step-by-step explanation:

a)

To solve this problem, we can use the equivalent of the suvat equations for a rotational motion.

In fact, the motion of the disk is a rotational motion with unifom angular acceleration.

So we can use the following suvat equation:

`\omega_f = \omega_i + \alpha t`

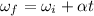
where:

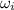`\omega_i` is the initial angular velocity

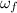`\omega_f` is the final angular velocity

`\alpha` is the angular acceleration

t is the time elapsed

In this problem:

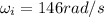`\omega_i = 146 rad/s` is the initial angular velocity

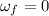`\omega_f=0`, since the disk comes to a stop

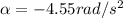`\alpha = -4.55 rad/s^2` (negative since the disk is slowing down)

Therefore, the time taken to stop is

`t=(\omega_f - \omega_i)/(\alpha)=(0-146)/(-4.55)=32.1 s`

b)

To solve this part of the problem, we can use another suvat equation for the rotational motion, which is:

`\theta = \omega_i t + (1)/(2)\alpha t^2`

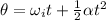
where

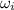`\omega_i` is the initial angular velocity

`\alpha` is the angular acceleration

t is the time elapsed

`\theta` is the angular displacement covered

For the disk in this problem:

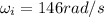`\omega_i = 146 rad/s` is the initial angular velocity

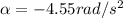`\alpha = -4.55 rad/s^2` (negative since the disk is slowing down)

t = 32.1 s (time elapsed, found in part a)

Substituting, we find the angle through which the disk has rotated in this time:

`\theta = (146)(32.1)+(1)/(2)(-4.55)(32.1)^2=2342 rad`