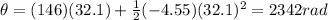a) 32.1 s
b) 2342 rad
Step-by-step explanation:
a)
To solve this problem, we can use the equivalent of the suvat equations for a rotational motion.
In fact, the motion of the disk is a rotational motion with unifom angular acceleration.
So we can use the following suvat equation:
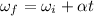
where:
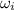 is the initial angular velocity
is the initial angular velocity
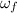 is the final angular velocity
is the final angular velocity
 is the angular acceleration
is the angular acceleration
t is the time elapsed
In this problem:
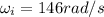 is the initial angular velocity
is the initial angular velocity
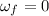 , since the disk comes to a stop
, since the disk comes to a stop
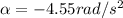 (negative since the disk is slowing down)
(negative since the disk is slowing down)
Therefore, the time taken to stop is
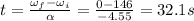
b)
To solve this part of the problem, we can use another suvat equation for the rotational motion, which is:
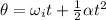
where
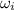 is the initial angular velocity
is the initial angular velocity
 is the angular acceleration
is the angular acceleration
t is the time elapsed
 is the angular displacement covered
is the angular displacement covered
For the disk in this problem:
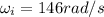 is the initial angular velocity
is the initial angular velocity
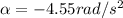 (negative since the disk is slowing down)
(negative since the disk is slowing down)
t = 32.1 s (time elapsed, found in part a)
Substituting, we find the angle through which the disk has rotated in this time: