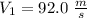Question

A Pitot-static probe is used to measure the speed of an aircraft flying at4000 m. Assume that the density of the atmosphere at that height is 0.82 kg/m3. Ifthe differential pressure reading is 3.5 kPa, determine the speed of the aircraft.

Answer 1

The speed of the aircraft is
`V_1 = 92.0 \ (m)/(s)`

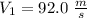
Step-by-step explanation:

Assumptions.

1. flow of air is steady & incompressible.

2. Frictional effects are neglected.

From the Bernoulli's equation

The velocity of the jet is given by

`V_(1) = \sqrt{2((P_2 - P_1)/(\rho)) }`

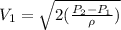
Here
`P_2 -P_1 = 3500 \ Pa`

`\rho = 0.82 (kg)/(m^(3) )`

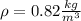
Thus velocity

`V_(1) = \sqrt{2((3500)/(\ 0.82)) }`

`V_1 = 92.0 \ (m)/(s)`

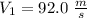
Therefore the speed of the aircraft is
`V_1 = 92.0 \ (m)/(s)`