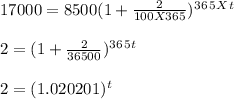Question

15. Jacob invests $8,500 in a savings account that promises a nominal rate of 2% continuously compounded.

(a) Write an equation for the amount this investment
would be worth after 1-years.
[3 points)
(b) How much would the investment be worth after
20 years?
14 points)
(c) Algebraically determine the time it will take for
the investment to double. Round to the nearest
tenth of a year.
[7 points]

Answer 1

(a)
`A = 8500(1+(2)/(36500))^3^6^5`

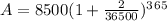
(b) A = $12680.37

(c)
`2 = (1.020201)^t`

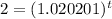
Step-by-step explanation:

Given:

Principal, P = $8,500

Rate of interest, r = 2%

Compounded continuously, n = 365

(a)

Time, t = 1

Amount, A equation = ?

We know:

`A = P(1 + (r)/(100 X n) )^n^t`

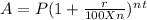
On substituting the value we get:

`A = 8500(1+ (2)/(100 X 365))^3^6^5 ^X ^1\\ \\A = 8500(1+(2)/(36500))^3^6^5`

(b)

Amount after 20 years = ?

t = 20

`A = 8500(1+ (2)/(100 X 365))^3^6^5 ^X ^2^0\\ \\A = 8500(1+(2)/(36500))^7^3^0^0\\\\\A = 12680.37`

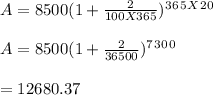
(c)

Amount to double = 8500 X 2

= $17000

Time, t = ?

`17000 = 8500(1+ (2)/(100 X 365))^3^6^5 ^X ^t\\ \\2 = (1+(2)/(36500))^3^6^5^t\\\\2 = (1.020201)^t`